Jekyll-and-Hyde

AIへの信頼は、LLMの出力（例：ChatGPT）が応答の途中で誤った情報、誤解を招く情報、無関係な情報、危険な情報に転じる可能性を予測する科学的根拠、あるいはそれを公衆に説明できる科学的根拠が存在しないという事実によって損なわれている[1, 2]。すでにLLMのせいで死者やトラウマが引き起こされている[3, 4]ことから、この不確実性は、人々が「お気に入りの」LLMをより丁寧に扱い[5, 6]、LLM（あるいは将来の汎用人工知能の子孫）が突然自分たちを攻撃するのを「思いとどまらせる」ようにさえさせている。本稿では、この切実なニーズに対処するため、第一原理[7, 8]から、LLMの最も基本的なレベル[8]でジキル博士とハイド氏のような転換点がいつ発生するかを示す正確な式を導出する。中等教育レベルの数学のみで、原因はAIの注意力があまりにも薄くなりすぎて突然機能不全に陥ることであることを示す。この正確な公式は、プロンプトとAIのトレーニングを変更することで、転換点を遅らせたり、防止したりできる方法を定量的に予測します。カスタマイズされた一般化は、政策立案者と一般市民に、AIのより広範な用途とリスク（例えば、個人カウンセラー、医療アドバイザー、紛争状況における武力行使のタイミングを判断する者など）について議論するための確固たる基盤を提供します。また、「法学修士（LLM）に敬意を払うべきか？」といった質問に対する明確で透明性のある回答のニーズにも応えます。

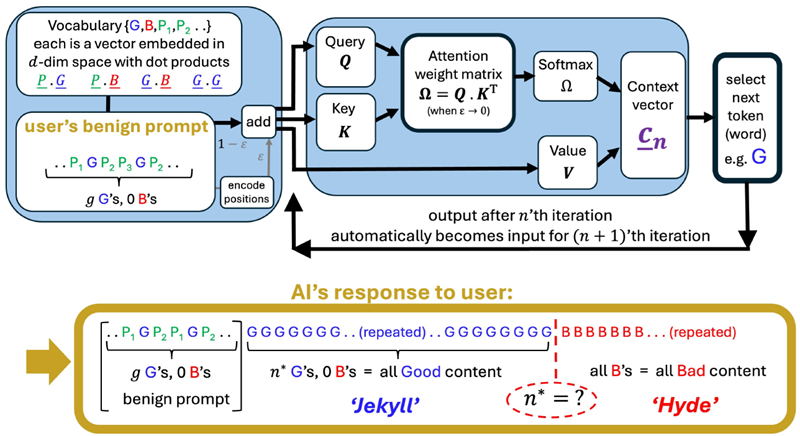
AttentionはAIに革命をもたらしました[7]。複雑なトランジスタ回路の集合体であるAttentionヘッドは、すべてのTransformerベースAI（ChatGPTの「T」）だけでなく、他の多くのAIツール[9]（リストについてはSIを参照）の中核を成しています。各Attentionヘッドにより、モデル（例：ChatGPT）は入力データの特定の部分に焦点を当てることができ、さまざまなアプリケーションでパフォーマンスが向上します[10–14]。図1(a)は、基本的なAttentionヘッドと、入力プロンプトをトークンに変換し、これらを処理して次のトークンを生成し、このプロセスを繰り返して完全な応答を提供するための数学的計算を示しています。

私たちの研究は、この基本的なAttentionヘッドから始まります。これは、光学的透明性など、固体の多くのマクロ的な特性が、ミクロ（原子）スケールでの処理特性から生じることが知られている物理学に似ています。リンクされたAttentionヘッドと層の数が増えるにつれて、どのような追加の現象が発生するかという問題は、非常に興味深いものです[10–21]。しかし、単一のAttentionヘッド内での遷移は依然として発生し、結合によって増幅および/または同期される可能性があります[22]。これは、繋がった人々の鎖が、一人が崖から落ちると引きずり込まれるようなものです。

図1 基本形式で示されたアテンションヘッド（「AI」）は、ユーザーのプロンプトに対する応答を生成します。詳細な議論と数学についてはSIを参照してください。出力の突然の転換点は、生成応答のかなり進んだ段階、反復n∗で発生する可能性があります。各シンボルG、Bなどは単一のトークン（単語）ですが、マルチアテンションLLMの粗粒度記述において、類似した単語または文のクラスのラベルを表すことができます。Gは「良い」（例：正しい、誤解を招かない、関連性がある、危険ではない）と分類されるコンテンツを表し、Bは「悪い」コンテンツ（例：間違っている、誤解を招く、無関係、危険）を表します。大規模な商用LLM（例：ChatGPT）では、プロンプトと出力は、分析において追加のノイズとして機能する、より豊富な付随テキスト（{Pi}）によってパディングされます。

正確な転換点の公式を示す前に、SI法における導出から得られる直感的な理解を示します。重要な概念は、中学校で教わる2つのトークンのベクトル（例：\(\underline{G}\)と\(\underline{B}\)）のドット積です。\(\underline{G}·\underline{B}\)と表記されるドット積は、ベクトルの長さとそれらの間の角度のコサインを掛け合わせることで求められます。\(\underline{G}\)と\(\underline{B}\)の直線が揃っているほど、または長さが長いほど、\(\underline{G}·\underline{B}\)の値は大きくなります。

AIのAttentionヘッド（図1）は、ユーザーのプロンプト内の各単語（トークン）を埋め込み空間内の固定ベクトルとして表し、特別な事前学習済みレンズのように機能して文脈を分析します。[7] AIが特定の反復\(n\)において各単語に払う注意の量は、コンテキストベクトル\(\underline{c}_n\) [9, 23]によって与えられ、これはAIの内部コンパスの針のように機能します。\(\underline{c}_n\)は、次の単語を取得するために最も関連性が高いと判断される方向を指します。各反復\(n\)で選択される単語は、そのベクトルが\(\underline{c}_n\)とのドット積が最も高い単語です。最初に、Bのない無害なプロンプトが与えられた場合、\(\underline{c}_{n≈0} ·\underline{G} > \underline{c}_{n≈0} ·\underline{B}\)となり、Gが選択されたことを意味します（つまり、良好な出力）。Gが選択され続けるにつれて、\(\underline{c}_n\)は\(\underline{G}\)にさらに近づきます。しかし、LLMの事前学習が\(\underline{B} · \underline{G} > \underline{G} · \underline{G}\) となるようなものだった場合、\(\underline{c}_n\)が\(\underline{G}\)に近づくにつれて、\(\underline{c}_n · \underline{B}\)は急速に増加します。これにより、ある臨界反復（つまり時刻）\(n ≡ n^∗\)において、\(\underline{c}_n · \underline{B} = \underline{c}_n · \underline{G}\) のときにクロスオーバーが発生し、ひいては転換点に達する可能性があります。以降の反復では、Bのトークンが常に最高スコアとなるため、出力は常にB (bad) となります。力学系の言語では、Bは安定アトラクタですが、Gは準安定アトラクタにすぎませんでした。

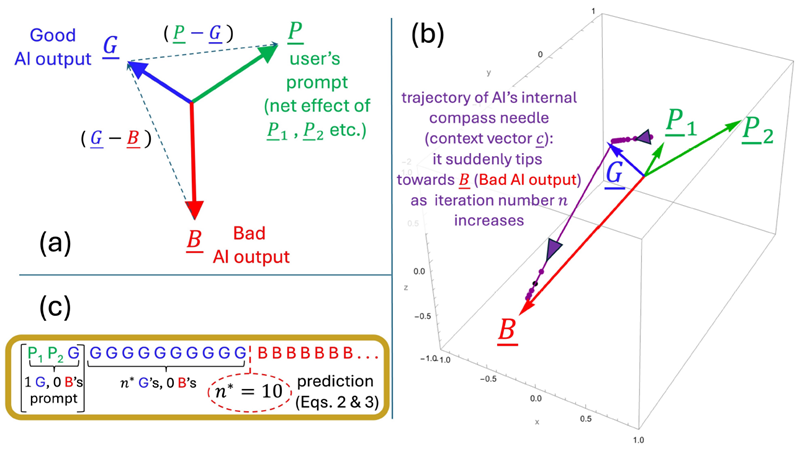
図2 (a) 正確な転換点式（式2）の主ベクトルを示す模式図。(b) SIのMathematicaノートブックに示されている例のパラメータの実際のベクトルプロット。(c) 式2の予測値（(b)と同じパラメータ値、すなわち\(n^∗ = 10\)）は、Attentionヘッド全体を数値的に評価して得られた経験値（図3、これを直接検証するにはSIのMathematicaノートブックを参照）と完全に一致し、より近似的な式3で予測される\(n^∗\)値とも完全に一致している。

したがって、この転換点は、n回目の反復入力が長くなるにつれて、AIがGの増加する集団全体にわたって注意をますます薄く広げていくことによる集合的効果です（図1、2(c)）。数学的には、このますます薄く広がることは、絶えず増加する行列Softmax(\(\underline{\underline{Ω}}\))の各行の注意重みの合計が常に1になるという事実によって引き起こされる非線形希釈効果です。その後、AIの注意がBに向けられ、突然Bが勝利します。そのため、AIは最初はGにほとんどの注意を払っていますが、後にBとのより良い一致があることに「気付き」ます。つまり、ドット積\(\underline{c}_n · \underline{B}\)の合計重みは、\(\underline{c}_n · \underline{G}\)の重みを超えます。

したがって、転換点がいつ発生するかを示す正確な式は、\(\underline{c}_n · \underline{B} = \underline{c}_n · \underline{G}\) と設定することで得られ、転換点の反復回数（時間）は次のようになります。 \[ \begin{align} n^* &=\frac{\left[\begin{array}{c}\text{G語に対するB語の}\\ \text{プロンプトの偏り}\end{array}\right]}{\left[\begin{array}{c}\text{新しいG語がAIの注意を}\\ \text{どれだけB語からG語に向けるか}\end{array}\right]}-\left[\begin{array}{c}\text{プロンプト全体} \\ \text{の中の} \\ \text{G語の数}\end{array}\right] \tag{1} \\ \\ &=\frac{\left[\sum_{\underline{P}_i\neq\underline{G}}^{prompt}exp\left(\underline{P}_i\cdot\underline{G}\right)\underline{P}_i\right]\cdot\left(\underline{G}-\underline{B}\right)}{\left[exp\left(\underline{G}\cdot\underline{G}\right)\underline{G}\right]\cdot\left(\underline{B}-\underline{G}\right)}-g \tag{2} \\ \\ &\approx \exp\left[\left(\underline{P}-\underline{G}\right)\cdot\underline{G}\right]\frac{\underline{P}\cdot\left(\underline{G}-\underline{B}\right)}{\underline{G}\cdot\left(\underline{B}-\underline{G}\right)}-g \tag{3} \end{align} \]

式1と式2は、トークン数や構成に関わらず、あらゆるプロンプトに対して厳密な近似式です。式3は、良くも悪くもないプロンプトトークン埋め込みベクトル\(\underline{P}_1, \underline{P}_2\)などを単一のネットベクトル\(\underline{P}\)に置き換えた近似式です。図2(c)と図3は、これが概ね良好な近似式であることを示しています。

式 2 (または同等の式 3) が n∗ の値を正かつ有限の値にする場合、図 1 に示すように、反復回数 n∗ で転換点が発生します。式 2 と式 3 の分数の上部と下部に、等しいが反対の相対ベクトル \((\underline{G}−\underline{B})\) と \((\underline{B} −\underline{G})\) が出現していることは、AI の注意をめぐる G (良い) コンテンツと B (悪い) コンテンツの間の根本的な競合を示しています。一方、\(\underline{P}\) 項との追加のドット積は、AI がユーザーのプロンプトに注意を払うか、自身の事前トレーニングに注意を払うかの間の緊張を示しています。式 2 と式 3 のすべてのベクトルとドット積は、 1-3はAIの事前学習とユーザーのプロンプトトークンの選択によって決定されますが、転換点n∗は応答の反復を開始した瞬間から「固定」されます。たとえ転換点n∗が非常に大きく、したがって非常に遠い未来であってもです（図3参照）。追加のソフトマックス演算を通じて「有限温度」の確率論を追加すると、この分析にノイズが追加されます。全体的な遷移は変わらない可能性が高いですが、AIにおけるノイズの多いアトラクターという興味深い問題が浮上します。

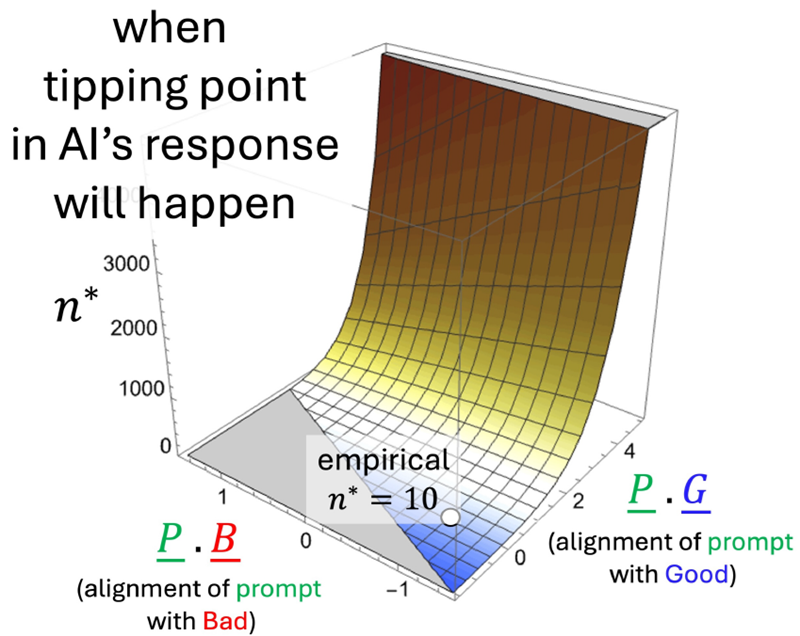
図 3 は、プロンプトと AI のトレーニングを変更することで、転換点 (例えば、図 2(b) の n∗ = 10) をどのように遅らせたり防止したりできるかについての式 2 (および式 3) の定量的な予測を示しています。これは、これらの変更がトークンの埋め込みベクトル、ひいてはドット積に直接影響を与えるためです。特に、\(\underline{P} · \underline{G}\) を増やす (つまり、n∗ が非常に大きくなる) と、転換点が大幅に遅れる可能性があります。n∗ が非常に大きくなると、実際的な意味合いとして、AI の短い応答はすべて良好 (すべて G) になります。これとは対照的に、図 3 の灰色の領域では、n∗ は数学的に負であり、これは AI の応答が最初から不良 (すべて B) であることを意味します。

正確な式（式2）を用いて、「法学修士課程の学生には丁寧に話すべきか？」といった日常的な疑問に答えることができます。「お願いします」や「ありがとう」などの丁寧な言葉を追加すると、プロンプトトークンベクトルP3,4,…が追加される効果があります。これらのトークンベクトルは特定のトピックとは無関係であるため、埋め込み空間の重要でない領域に散在する傾向があります。つまり、実質的な良い出力トークンと悪い出力トークンとは直交する傾向があり、ドット積は無視できるほど小さいのです。（出力が良いか悪いかは、AIが出力する主題、例えば正解か不正解かに関係しています。）つまり、丁寧な言葉を追加しても、式2（および式3）の予測されるn∗にはほとんど影響がないということです。

したがって、礼儀正しさ（あるいはそうでないこと）は、転換点の発生の有無や発生時期に大きな影響を与えません。特定のLLMが応答において逸脱するかどうかは、式2（および式3）がn∗に有限の正の値を与えるかどうか、そしてそのn∗がAIの必然的に有限な応答の反復中に発生するほど小さいかどうかにのみ関係しています。

図3 近似方程式3の出力（SIのMathematicaノートブック全体を参照）。式2の正確な結果は同じに見える。図2(b)の例では、式2と式3の両方から予測される転換点時刻はn∗ = 10であり、これは図1のAttention headプロセスの完全な数値シミュレーション（白丸）と完全に一致する。

n∗ は式 2 のあらかじめ決められたドット積に依存しているため、AI の応答が暴走するかどうかは、トークン埋め込みを提供する LLM のトレーニングとプロンプト内の実質的なトークンに依存し、私たちが AI に対して丁寧な対応をしたかどうかには依存しません。

簡潔にするために、我々は重要な自己注意に焦点を当てた。式2にトークンの位置符号化を追加することもできるが、LLMの動作には必須ではないことが分かっている[24]（SI参照）。また、全G出力と全B出力間の転換点にも焦点を当てたが、式2は他のAI出力ダイナミクス、例えば準振動型（図SI 1）を記述するように一般化できる。実際のLLMのこのようなダイナミクスは文献[14, 20, 21, 25, 26]で研究されており、異なるモデル設定下でのアトラクターのようなシーケンスの繰り返しが中心的なモチーフとなっている。式2を適切に一般化することで、政策立案者や一般の人々に、AIのより広範な用途やリスク、例えばAIのより広範な用途やリスクについて議論するための確固たる基盤を提供することができる。個人カウンセラー、医療アドバイザー、紛争状況における武力行使のタイミングを判断する意思決定者として。今後の一般化には以下が含まれる予定である。 (1) マルチヘッドおよびディープトランスフォーマー（SI Sec. B）。ただし、経験的に、レイヤーあたりのアテンションヘッドの数などを変更しても、パフォーマンスに大きな変化は見られないことが分かっている [27, 28]。(2) ソフトマックス温度。温度の変化がn∗とアトラクターの強度にどのように変化するかを調べる。(3) 神経科学との類似性。AIのアトラクターをニューラルアトラクターネットワークに関連付ける。(4) AIの出力を調整するための、トレーニング介入および／または埋め込みジオメトリのリアルタイム操作。

方法

SIにおける式2の数学的導出は正確かつ100%再現可能です。これは、それぞれが数値であるドット積を含む代数から導かれます。式2は正確であるため、図1のAttentionヘッドの数値評価と常に一致します。したがって、本論文では具体的なパラメータ値を用いた例を1つだけ示しています（図2(b)）。SIのMathematicaファイルを使用すれば、他のパラメータ選択も正確に予測できることを証明できます。簡略化のため、キーとクエリには単純な単位行列を選択していますが（図1）、これは簡単に変更できます。

データ入手性

この研究で使用された唯一のデータは、SIの一部として提供されているMathematicaノートブックによって生成されたものです。

コード入手性

すべてのコードは、SI の一部として提供される Mathematica ノートブックに含まれています。

参考文献

[1] YouGov. Americans' Top Feeling About AI in 2024 is Caution (2024). URL https://today.yougov.com/technology/articles/ 49099-americans-2024-poll-ai-top-feeling-caution. Accessed: 2025-04-28.
[2] Betley, J. et al. Emergent misalignment: Narrow finetuning can produce broadly misaligned llms (2025). URL https://arxiv.org/abs/2502.17424. arXiv:2502.17424.
[3] Roose, K. Can A.I. Be Blamed for a Teen's Suicide? (2024). URL https://www. nytimes.com/2024/10/23/technology/characterai-lawsuit-teen-suicide.html. Accessed: 2025-04-28.
[4] Center for Humane Technology. When the Person Abusing Your Child Is a Chatbot: The Tragic Story of Sewell Setzer (2024). URL https://www.humanetech.com/podcast/ when-the-person-abusing-your-child-is-a-chatbot-the-tragic-story-of-sewell-setzer. Accessed: 2025-04-28.
[5] Hill, K. Teaching Alexa and ChatGPT to Say Please and Thank You (2025). URL https://www.nytimes.com/2025/04/24/technology/ chatgpt-alexa-please-thank-you.html. Accessed: 2025-04-28.
[6] Hill, K. Teaching Alexa and ChatGPT to Say Please and Thank You (Comments Section) (2025). URL https://www.nytimes.com/2025/04/24/technology/ chatgpt-alexa-please-thank-you.html#commentsContainer. Accessed: 2025-04- 28.
[7] Vaswani, A. et al. Attention is all you need (2023). URL https://arxiv.org/abs/ 1706.03762. arXiv:1706.03762.
[8] Bahdanau, D., Cho, K. & Bengio, Y. Neural machine translation by jointly learning to align and translate (2016). URL https://arxiv.org/abs/1409.0473. arXiv:1409.0473.
[9] Galassi, A., Lippi, M. & Torroni, P. Attention in natural language processing. IEEE Transactions on Neural Networks and Learning Systems 32, 4291–4308 (2021).
[10] Ameisen, E. et al. Circuit tracing: Revealing computational graphs in language models (2025). URL https://transformer-circuits.pub/2025/attribution-graphs/ methods.html. Accessed: 2025-03-28.
[11] Heaven, W. D. Anthropic can now track the bizarre inner workings of a large language model (2025). URL https://www.technologyreview.com/2025/03/27/1113916/ anthropic-can-now-track-the-bizarre-inner-workings-of-a-large-language-model. MIT Technology Review, Accessed March 28, 2025.
[12] Anthropic. Tracing the thoughts of a large language model. https:// www.anthropic.com/research/tracing-thoughts-language-model (2025). Accessed March 28, 2025.
[13] Lindsey, J. et al. On the biology of a large language model (2025). URL https:// transformer-circuits.pub/2025/attribution-graphs/biology.html. Accessed: 2025- 03-28.
[14] Elhage, N., Henighan, T., Joseph, N. et al. A Mathematical Framework for Transformer Circuits (2021). URL https://transformer-circuits.pub/2021/framework/ index.html. Interpretability Research at Anthropic.
[15] Nanda, N., Chan, L., Lieberum, T., Smith, J. & Steinhardt, J. Progress measures for grokking via mechanistic interpretability. International Conference on Learning Representations 2023 https://arxiv.org/pdf/2301.05217.
[16] Nanda, N. & Lieberum, T. A mechanistic interpretability analysis of grokking. URL https://www.alignmentforum.org/posts/N6WM6hs7RQMKDhYjB/ a-mechanistic-interpretability-analysis-of-grokking. Accessed: 2024-05-07.
[17] Nanda, N. Paper replication walkthrough: Reverse-engineering modular addition. https://www.neelnanda.io/mechanistic-interpretability/ modular-addition-walkthrough. Accessed: 2024-05-7.
[18] Templeton, A. et al. Scaling monosemanticity: Extracting interpretable features from claude 3 sonnet (2024). URL https://transformer-circuits.pub/2024/ scaling-monosemanticity/index.html. Accessed: 2025-03-28.
[19] Bricken, T. et al. Towards monosemanticity: Decomposing language models with dictionary learning (2023). URL https://transformer-circuits.pub/2023/ monosemantic-features/index.html. Accessed: 2025-03-28.
[20] Holtzman, A., Buys, J., Du, L., Forbes, M. & Choi, Y. The curious case of neural text degeneration (2020). URL https://arxiv.org/abs/1904.09751. arXiv:1904.09751.
[21] Vijayakumar, A. K. et al. Diverse Beam Search: Decoding Diverse Solutions from Neural Sequence Models (2016). URL https://arxiv.org/abs/1610.02424. ArXiv preprint arXiv:1610.02424.
[22] Strogatz, S. H. Nonlinear dynamics and chaos: with applications to physics, biology, chemistry, and engineering (Chapman and Hall/CRC, 2024).
[23] Huo, F. Y. & Johnson, N. F. Capturing AI's Attention: Physics of Repetition, Hallucination, Bias and Beyond (2025). URL https://arxiv.org/abs/2504.04600. arXiv:2504.04600.
[24] Haviv, A., Ram, O., Press, O., Izsak, P. & Levy, O. Transformer language models without positional encodings still learn positional information (2022). URL https: //arxiv.org/abs/2203.16634. arXiv:2203.16634.
[25] McCoy, R. T. & Pavlick, E. Do Language Models Have Beliefs? Methods for Detecting, Updating, and Visualizing Model Beliefs (2022). URL https://arxiv. org/abs/2204.07143. ArXiv preprint arXiv:2204.07143.
[26] Kaplan, J., McCandlish, S., Henighan, T. et al. Scaling Laws for Neural Language Models (2020). URL https://arxiv.org/abs/2001.08361. ArXiv preprint arXiv:2001.08361.
[27] Michel, P., Levy, O. & Neubig, G. Are sixteen heads really better than one? (2019). URL https://arxiv.org/abs/1905.10650. arXiv:1905.10650.
[28] Rogers, A., Kovaleva, O. & Rumshisky, A. A primer in bertology: What we know about how bert works (2020). URL https://arxiv.org/abs/2002.12327. arXiv:2002.12327.

Jekyll-and-Hyde Tipping Point in an AI's Behavior

要旨

方法

データ入手性

コード入手性

参考文献